| ||||||
ABC tables are very easy to use and more than adequate for the bearing of a celestial body. These tables avoid the need to use a calculator or Log tables but are based on the previous formulae. The Rules may seem unwieldy at first but they are printed on each page and quickly become automatic. These transpose the Azimuth formula so that A = Tan(Lat) / Tan(LHA) B = Tan(Dec) / Sin(LHA) C = Difference A ~ B = 1/ [Tan(Azimuth) x Cos(Lat) ]
Example Latitude 20° N Declination 45° S LHA 30°
A 0.63 S Opposite to Latitude unless LHA > 180° B 2.00 S Same as Declination -------- C 2.63 S Same name; Sum. Different names; Difference The C Table gives a bearing of 22°.0. The sign of C means that this bearing is south. It is west because the LHA is less than 180°. The C result would normally be written as "S 22°.0 W" or 158°. The effect of rounding ABC Tables’ values is negligible (+/- 0°.1) This is not true of the older Sight Reduction Tables where the calculated altitude is rounded to the nearest minute. Furthermore the need to use a plotting sheet with a rounded, estimated position provides considerable scope for inaccuracy. (Sight Reduction Tables were known as the Air Navigation Tables until 2003.) The author’s preferred manual method is a calculator for the Zenith Distance and ABC tables for Azimuths. Without a calculator he would still use the Cosine formula but with log tables. | ||||||
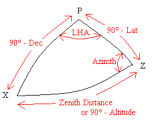
The difference between the True (TZD) and Calculated (CZD) Zenith Distances is the Intercept. TRUE, TINY, TOWARDS If the TZD is less than the CZD then the assumed position must be moved in the direction of the body by the amount of the Intercept. This gives a position of the correct distance from the body. It is known as the Intercept Terminal Position or ITP. As the radius of the circle is normally very large, it is considered to be a straight line near this point. A line at 90 to the direction of the body is the Position Line.
A single Position Line must be combined with other observations for a fix. This can be achieved using a plotting sheet and then transferring the ITP by the distance to the next sight and redrawing the Transferred Position Line in the same direction as the original. For Sun sights, it is more usual to calculate the ITP of a morning sight and then calculate the transferred position for the Sun's Meridian Passage (Noon.) The difference between calculated and observed latitudes provides a longitude using “Plane Sailing.” With a little practice, this will be found to be a faster, not to mention more accurate method. For Star Sights, many people use a single position and then plot the Position Lines without allowing for the vessel's movement. This may appear a sloppy practice but a few miles error mid-ocean is usually irrelevant. Even if the position at sunset was perfect, there is no guarantee that the position an hour later is within a mile. Indeed even if the position agrees perfectly with a GPS position, there is no guarantee that an intervening military operation has not thrown the GPS position out let alone a fault in the equipment/ aerial. “I am about here,” is a far safer assumption than “My wheelhouse is/ was within 10m of this position.” | ||||||
Next Section Corrections to a Sextant Altitude
| ||||||
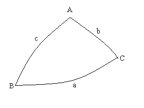
To Calculate a Side - The Cosine Formula Cos(a) = Cos(b) x Cos(c) + Sin(b) x Sin(c) x Cos(A) Applying this to the PZX triangle we get:- Cos(Zenith Distance) = Cos(co-Lat) x Cos(co-Dec) + Sin(co-Lat) x Sin(Co-Dec) x Cos(LHA)
Because Sin(co-A) = Cos(A) and Cos(co-A) = Sin(A) Cos(Zenith Distance) = Sin(Lat) x Sin(Dec) + Cos(Lat) x Cos(Dec) x Cos(LHA) If Altitude is preferred; Zenith Distance = co-Altitude thus Sin(Altitude) = Sin(Lat) x Sin(Dec) + Cos(Lat) x Cos(Dec) x Cos(LHA)
For an Angle Tan(C) = Sin(A)/ [Sin(b)/ Tan(c) – Cos(b) x Cos(A)] Inserting terms from the PZX triangle this becomes Tan(Az) = Sin(LHA)/ [Sin(co-Lat)/ Tan(co-Dec) – Cos(co-Lat) x Cos(LHA)] Or Tan(Az) = Sin(LHA)/ (Cos(Lat) x Tan(Dec) – Sin(Lat) x Cos(LHA))
The Spherical Sine Formulae Sin(a)/ Sin(A) = Sin(b)/ Sin(B) = Sin(c)/ Sin(C)
| |
These can be used when one of the sides or angles is 90°. | |
 | |||||
If angle A is 90° then a diagram is drawn with A above the circle and the sectors filled with the adjoining sides. | |||||
 | |||||
Notice that the three sectors of the lower half are marked “co-” In other words the compliment of these angles is used. The two formulae are; Sin(Mid Part) = Tan (Adjacent Parts) e.g. Sin(c) = Tan(co-B) x Tan(b) or Sin(c) =Cot(B) x Tan(b) And Sin (Mid Part) = Cos(Opposite Parts) e.g. Sin(c) = Cos(co-a) x Cos(co-C) or Sin(c) = Sin(a) x Sin(C)
| |||
Example using Napier’s Rules Assume that the True Altitude is 0° therefore the Zenith Distance is 90°. | |||
 | |||
 | |||
Co-Dec is the mid-part therefore the two opposites are Azimuth and co-Lat. Sin (Mid Part) = Cos(Opposites) Sin(co-Dec) = Cos(Azimuth) x Cos(co-Lat)
Cos(Dec) = Cos(Azimuth) x Sin(Lat) Cos(Azimuth) = Sin(Dec)/ Sin(Lat)
The Amplitude of a body is measured from East or West rather than North. In other words Amplitude = 90° - Azimuth = co-Azimuth. Sin(Amplitude) = Sin(Dec)/ Sin(Lat) This gives the formula that many readers will be familiar with of Sin(Amplitude) = Sin(Dec) x Sec(Lat)
|
END OF TUTORIAL
|